鸡兔同笼二元一次方程解法（鸡兔同笼方程解法详解，快速解题技巧）

鸡兔同笼：解密二元一次方程的奥妙

在古老的，流传着一个关于“鸡兔同笼”的有趣故事：一只鸡和一只兔子同住在一个笼子里，结果它们的头和脚总数都让人琢磨不透。这个问题不仅是儿童智力游戏的经典题材，更是二元一次方程的实际应用。这一题目，我们不仅能够锻炼解决实际问题的能力，也能见识到数学的魅力。本文将围绕“鸡兔同笼”这一数学模型，深入探讨二元一次方程的解法，并具体实例帮助读者更好理解这一主题。

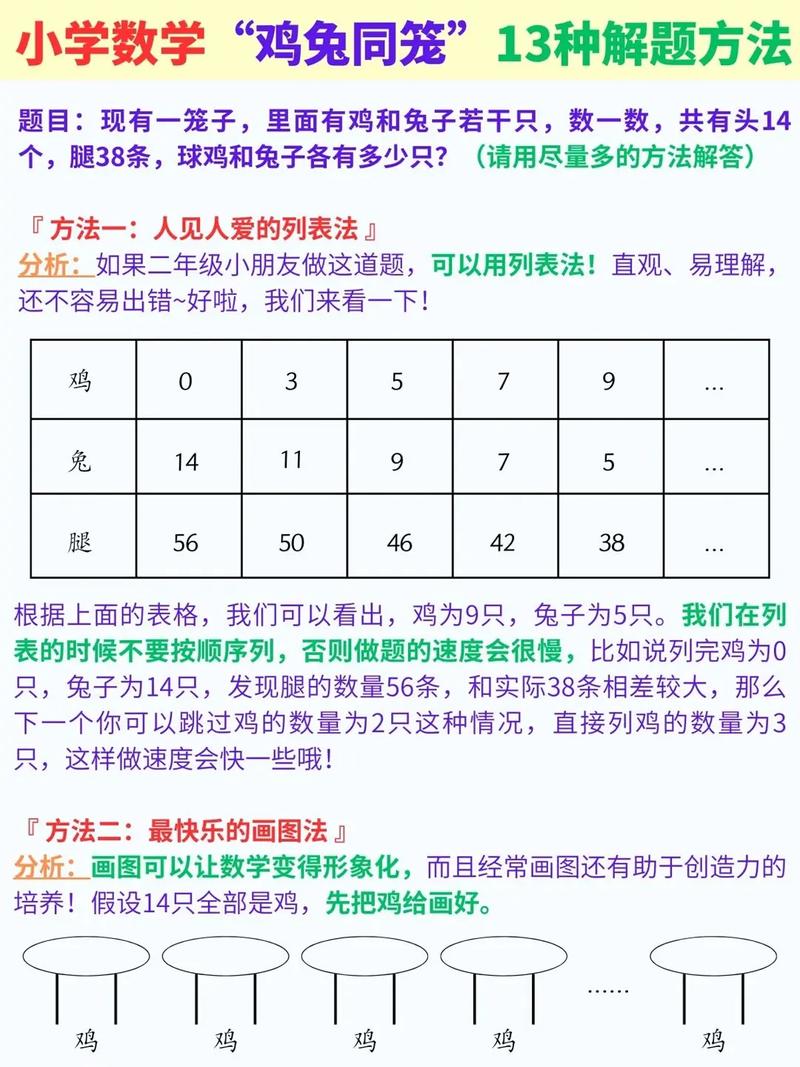
鸡兔同笼的问题背景

鸡兔同笼问题的基本设定是：已知笼子里鸡和兔子的总数，以及它们的脚的总数，求鸡和兔子的数量。公式可以用以下方式表示：设鸡的数量为 x，兔子的数量为 y，那么可以建立两个方程：

1. x + y = 总动物数

2. 2x + 4y = 总脚数

这些方程汇集了现实生活中的简单计算，这些简单的数学工具，我们可以解决看似复杂的问题。

建立方程：从数值到变量

为了更好地理解这个问题，我们可以一个具体的例子来展示如何设置方程。假设笼子里总共有35只动物，其中有134只脚。那么：

1. x + y = 35

2. 2x + 4y = 134

此时，我们需要对这两个方程进行分析，找出解决方案。

运用代入法解方程

在这两个方程中，可以利用代入法来简化计算。从第一个方程中，我们可以解出变量 y：

y = 35 - x

接下来，将这个表达代入到第二个方程中：

2x + 4(35 - x) = 134

化简后，我们可以得到：

2x + 140 - 4x = 134

-2x + 140 = 134

-2x = -6

x = 3

现在已知 x 的值为3，接下来可以求出 y：

y = 35 - 3 = 32

以上步骤，我们得到了问题的答案：笼中有3只鸡和32只兔子。

与意义

鸡兔同笼的问题不仅是一个简单的数学计算题，它实际上是二元一次方程应用的典型案例。这样的实例，读者能够看到数学的逻辑之美和结构。对于学生来说，理解这类问题可以帮助提升逻辑思维能力和解题技巧。对于生活中的实际问题，这种数学模型的运用可以成为解决问题的重要工具，让我们更好地理解和应用数学。对鸡兔同笼题目的分析，我们不仅掌握了一种求解方法，也深化了对二元一次方程的认识，从而为今后的数学学习打下坚实的基础。

在这个快速变化的时代，数学不仅仅是一门学科，它更是一种思维方式和解决问题的工具。无论是用在生活中，还是在更高级的学术探讨中，掌握基本的数学模型和解法都将是我们前行的坚实助力。