拐点的定义是二阶导数等于零（拐点识别：二阶导数零点揭秘）

拐点的定义是二阶导数等于零——探寻函数变化的关键点

在数学的世界里，拐点是一个充满魅力的概念，承载着无数现实与抽象交织的情感。在函数图像的波动中，拐点呈现为改变趋势的重要分水岭。正如人生的变迁，理解拐点的深意，能够让我们更清晰地看待变化带来的机遇与挑战。本文将深入探讨何为拐点，以及其与二阶导数的关系，让我们在这一过程中发掘数学的美妙与哲理。

拐点的数学定义

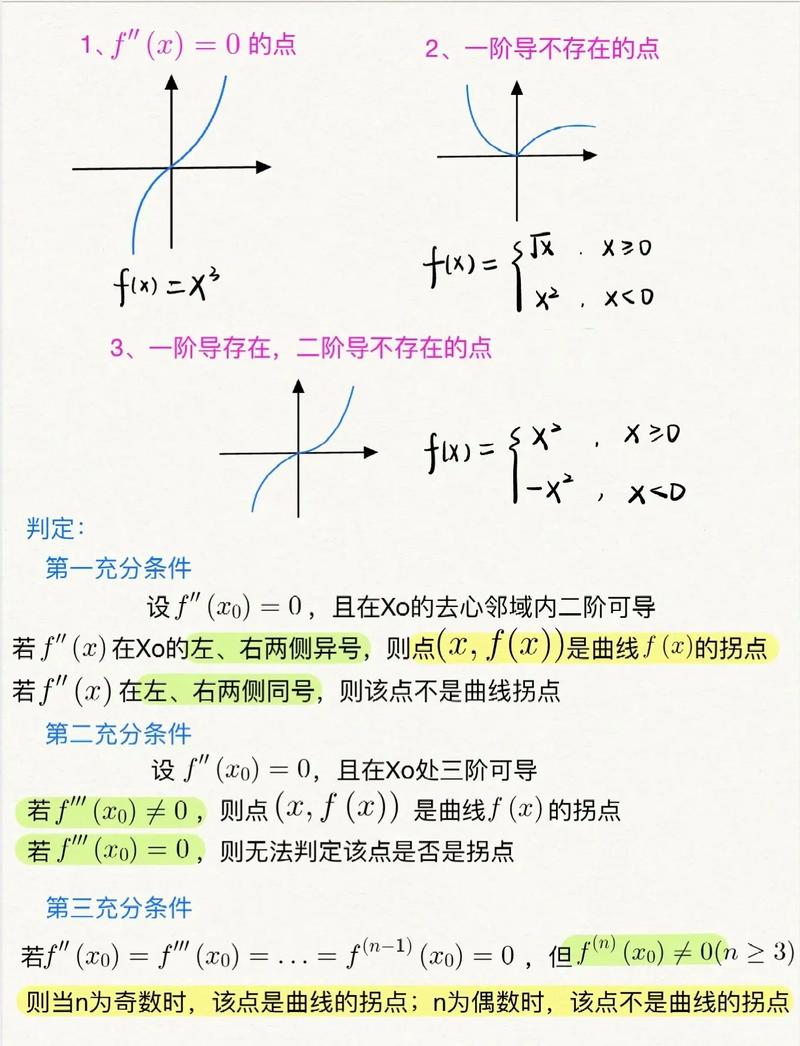
在微积分的领域，函数的拐点是其图形变化方向发生改变的点。更准确地说，拐点发生在函数的二阶导数等于零的地方。简单来说，如果一个函数在某个点处的二阶导数是零，意味着其一阶导数（即切线的斜率）在这个点附近可能发生变化。虽然二阶导数为零是拐点存在的必要条件，但并不是充分条件——这还需要判断一阶导数的符号变化。

二阶导数与拐点的关系

二阶导数不仅仅是衡量函数曲率的工具，更是判断拐点的重要指标。当我们说“二阶导数等于零”时，我们是在探讨函数图形的弯曲程度。如果这个导数值为正，函数向上凹；如果为负，函数向下凹。只有在二阶导数等于零的点，我们才能探寻是否存在着拐点的可能。拐点的真实存在，还需要观察一阶导数的变化来进行验证。

举个简单的例子，考虑二次函数 \( f(x) = ax^二 + bx + c \)。该函数的二阶导数 \( f''(x) = 二a \) 永远是正数（\( a > 零 \)）或负数（\( a < 零 \)），因此在这个情况下并不会存在拐点。而对于 \( f(x) = x^三 \) 来说，其二阶导数 \( f''(x) = 六x \)，在 \( x = 零 \) 时，二阶导数为零，且该点是一个拐点，因为一阶导数在此处从负变正，表示函数在此处由凹变凸。

拐点的实际意义

拐点不仅仅存在于抽象的数学理论中，它在现实世界中同样具有重要的意义。对于经济学家而言，拐点可以帮助识别经济周期的转折点；在金融市场上，股票价格的拐点则可能暗示投资者的买入或卖出信号。社会学中，研究趋势变化的拐点有助于理解公共意见的转变。

例如，在技术创新的早期阶段，企业可能面临着市场需求的快速变化，理解这些变化的拐点，能够让企业更好地调整产品策略以适应市场需求。这种调节反应与数学中的拐点相似，都是关于如何在变化中找到新的方向，抓住机会。

理解“拐点的定义是二阶导数等于零”这一概念，不仅有助于掌握数学中的微分学，更让我们意识到变化在生活中的重要。无论是科学研究还是日常决策，拐点提醒我们关注与探索那些看似平静但潜藏变革的瞬间。对拐点的深入理解，我们将能更有效地在复杂的世界中导航，识别出变化背后的规律与趋势，从而为未来的选择奠定坚实的基础。