最大公约数怎么求算法（快速求解最大公约数算法全解析）

最大公约数的求解算法

在数学中，最大公约数（）是指能够整除两个或多个整数的最大正整数。求解最大公约数的算法在数论、计算机科学以及日常生活中都有着广泛的应用。无论是简化分数、解决数学问题，还是在编程中处理数据，了解如何高效地计算最大公约数都是一项重要的技能。本文将探讨几种常见的求解最大公约数的算法，帮助读者更好地理解这一概念。

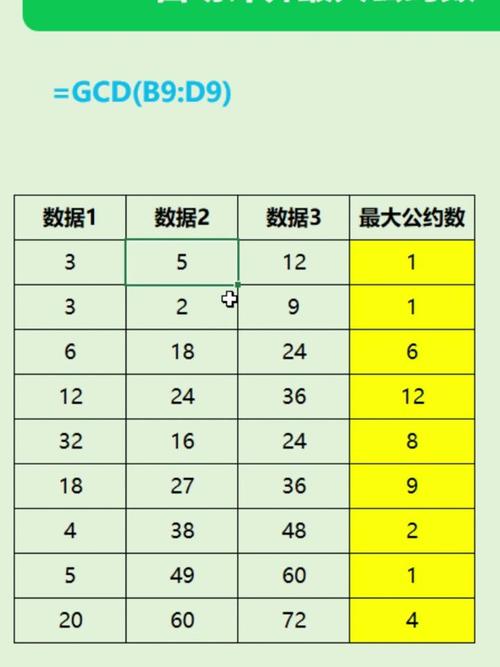
欧几里得算法

欧几里得算法是求解最大公约数最经典的方法之一。它的基本思想是利用两个数的余数来逐步缩小问题的规模。具体步骤如下：

1. 设有两个正整数a和b（假设a > b）。
2. 计算a除以b的余数r。
3. 如果r为零，则b即为最大公约数；如果r不为零，则将b赋值给a，将r赋值给b，重复步骤二。

这种方法的时间复杂度为O(log(min(a, b)))，在实际应用中非常高效。

更相减损法

另一种求解最大公约数的方法是更相减损法。该方法的核心思想是不断减去较小的数来找到最大公约数。具体步骤如下：

1. 设有两个正整数a和b。
2. 如果a等于b，则a（或b）即为最大公约数。
3. 如果a大于b，则用a减去b，得到新的a；如果b大于a，则用b减去a，得到新的b。
4. 重复以上步骤，直到a等于b。

虽然这种方法直观，但在处理较大的数时效率较低，因此在实际应用中不如欧几里得算法常用。

利用质因数分解

质因数分解也是求解最大公约数的一种方法。将两个数分解为质因数，可以找出它们的共同因数，从而计算出最大公约数。具体步骤如下：

1. 将两个数分别进行质因数分解。
2. 找出它们的共同质因数。
3. 将共同质因数的最低次幂相乘，得到最大公约数。

尽管这种方法在理论上可行，但在实际计算中，由于质因数分解的复杂，通常不如前两种方法高效。

编程实现

在编程中，求解最大公约数的算法可以多种语言实现。以下是使用Python语言实现欧几里得算法的示例代码：

这段代码简单明了，利用了欧几里得算法的思想，能够快速计算出两个数的最大公约数。

最大公约数的求解算法在数学和计算机科学中具有重要意义。了解和掌握欧几里得算法、更相减损法以及质因数分解等方法，读者可以在不同场景下灵活运用，提升解决问题的能力。无论是在学术研究还是日常生活中，最大公约数的计算都能帮助我们更好地理解数字之间的关系。